Re:ゼロから始めるML生活

どちらかといえばエミリア派です

【写経】ニューラルネットワークについて勉強してみた

ニューラルネットワーク Python

この前は、ニューラルネットワークのふわっとした概要だけ勉強しました。

tsunotsuno.hatenablog.com

勉強してた本はこちら。

bookmeter.com

正直、勉強している本の著者が書いたコードがgithubにあるのでやる気はなかったのですが、 最初のうちは馬鹿正直に見よう見まねで実装してみるのもありかと思ったのと、そもそもPython初心者なのでPythonの勉強も兼ねて、見よう見まねで実装（ほぼ写経）しました。

前回は理論について紹介したので、今回は実装について取り上げます。

※ちゃんとコード書いた証明にgithubにあげときます。あんまりきれいじゃないですが、気にしない気にしない。。。

github.com

実装の事始め

著者の方の実装を参考になんとなく実装しました。 特徴としては、関数ごとにPythonのクラスを作成しています。 順伝播と逆伝播のメソッドを備えたクラスを用意して、それを順番にガッチャンコしていって実装します。

まずイメージとしては、下の図のような2層ニューラルネットワークを作成します。

f:id:nogawanogawa:20171223163954j:plain:w400

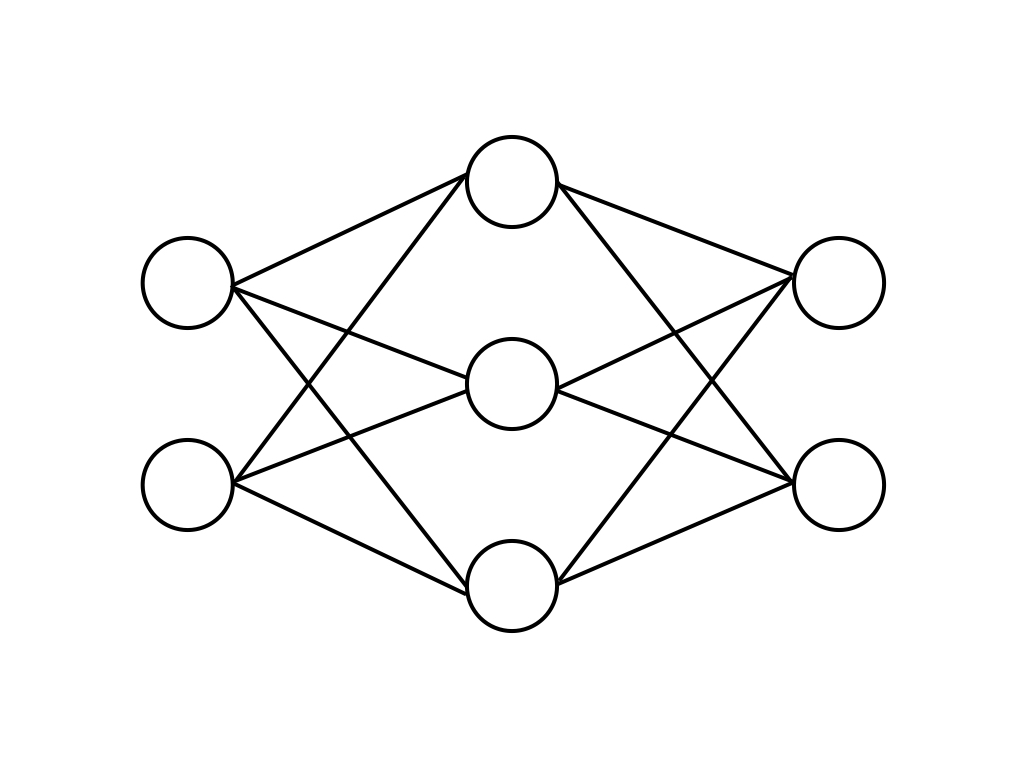
これをクラスのつながりで表現するとこんな感じ。

なので、今回の簡単実装では出てクラスは主に下のような感じです。

  • Affine
  • Sigmoid
  • Softmax

3層以上のネットワークを作成しようと思っても、この実装だとガッチャンコするクラスの数を変えればいいだけなので、 使いたい分だけ勝手にカスタムできます。 あとで別の活性化関数を使用したかったりしたら、そこだけ置き換えれば動くはずです。

では、少しずつ中身を見ていきます。

MNIST

まず、今回使用するデータはニューラルネットで使用されるサンプルデータセットであるMNISTです。

f:id:nogawanogawa:20180108091704p:plain

上図のように、手書きの数字の図（28×28）とその正解の数字が格納されています。

読み込んで使用するときは意外と簡単で、下のような1行で読み込みができます。

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

色々パラメータをしていますが、細かいことは本読んでみてください。←

簡単に使えるっていう雰囲気がわかったところで次に進みます。

Affine

前回さらっと言ってしまったのですが、ニューラルネットの計算のときに入力とリンクの重みを掛け合わせる行列積が出てきました。 幾何学的に言うとこれをAffine変換と言うそうです。

forward

前回は行列積しか紹介しませんでしたが、実際には特定の方向に強引に引き寄せるバイアスも入ってきます。 ですので、式としてはこんな感じになります。

{ \displaystyle Y=A \cdot X + B }

順伝播ではこれを計算します。

def forward(self, x):
    # 入力の形状を読み取って記録に残す
    self.original_x_shape = x.shape
    x = x.reshape(x.shape[0], -1)
    self.x = x

    #affine変換
    out = np.dot(self.x, self.W) + self.b

    return out

意外と簡単に書いていますね。最初の3行はbackwardで使うための準備で、 入力の値と行列の形状をオブジェクトに記録しています。 値を記録しているのは、逆伝播の際に順伝播の際の入力を使用するためです。 形状を記録するのは、backwardのときに行列を転置する必要があるためで、逆伝播の計算をした後行列を元の形状に戻すのに使用しています。

backward

Affine層では直前の層への入力と自分の層の重みの更新量を計算する必要があります。

Affine変換について逆伝播するときには、式としてはこんな感じになります。

{ \displaystyle \frac{\partial L}{\partial W} = X^{T} \cdot \frac{\partial L}{\partial Y} }

絵で書くとこんな感じです。

f:id:nogawanogawa:20180112221157j:plain

書いてみるとこんな感じです。

def backward(self, dout):
    dx = np.dot(dout, self.W.T)

    #更新する重みの差分量計算                                                                                                                     
    self.dW = np.dot(self.x.T, dout)
    self.db = np.sum(dout, axis=0)

    #直前の層への入力                                                                                                                             
    dx = dx.reshape(*self.original_x_shape)  # 入力データの形状に戻す（テンソル対応）                                                                         
    return dx

Affine層に直前の層がある場合には、そちらの層への左向きの入力が必要になるのでそちらも計算します。

Sigmoid

順伝播でAffine変換をしたあとは、活性化関数によって発火をします。 今回は活性化関数としてSigmoid関数を使用します。

forward

Sigmoid関数は式で書くと下のようになっていました。

{ \displaystyle y=\frac{1}{1+e^{-x}} }

図で書くとこんな感じです。

f:id:nogawanogawa:20171224091711p:plain

これを書いて見るとこんな感じになります。

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def forward(self, x):
    out = sigmoid(x)
    self.out = out
    return out
backward

Sigmoid関数自体は重みとか関係ないので、直前の層への入力の計算だけになります。 直前の層への入力は下のような感じになります。

{ \displaystyle \frac{\partial L}{\partial y} y(1-y) }

コードを書いてみるとこんな感じ。

    def backward(self, dout):
       return dout*(1.0 - self.out) * self.out

Softmax

分類問題の順伝播で出力層では、確率分布を算出するため、出力の総和を1になるように出力をならす必要があります。 今回は簡単な方法としてSoftmax関数をかませます。

forward

Softmax関数を式で表すとこんな感じです。

{ \displaystyle y_k = \frac{e^{a_k}}{\sum_{i=1}^{n} e^{a_i}} }

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0) # オーバーフロー対策①                                                                                                          
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x) # オーバーフロー対策②                                                                                                                      

    return np.exp(x) / np.sum(np.exp(x))

ソフトマックス関数では、値がxの値が大きすぎるとべき乗計算をする関係で計算が簡単にオーバーフローします。 そのため、オーバーフローしないように、上の実装ではオーバーフローしないように工夫してあります。

次に、損失関数を計算しています。 損失関数としては、クロスエントロピー関数を使用しています。 （詳細は省略します）

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換                                                                                            
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

上の２つの関数を使用すると、こんな感じのforwardになります。

def forward(self, x, t):
    self.t = t
    self.y = softmax(x)
    self.loss = cross_entropy_error(self.y, self.t)

    return self.loss
backward

Softmax関数でも、Sigmoid関数と同様に、直前の層に対する入力を計算するだけです。 計算する値は下のようになります。

{ \displaystyle \frac{\partial L}{\partial y} y(1-y) }

def backward(self, dout=1):
    batch_size = self.t.shape[0]

    if self.t.size == self.y.size :
        dx = (self.y - self.t) / batch_size
    else :
        dx = self.y.copy()
        dx[np.arange(batch_size), self.t] -= 1
        dx = dx / batch_size

    return dx

ちゃんと動けば、こんな感じの学習途中の検出精度のグラフが出ます。

f:id:nogawanogawa:20180113083857p:plain

感想

Pythonはふわっと書けるのがいいですね。お手本があると意外と簡単に書けます。

そろそろ難しいことやらないとなあ。。。